
It is also worth noting that the position of the orthocenter changes depending on the type of triangle for a right triangle, the orthocenter is at the vertex containing the right angle for an obtuse triangle, the orthocenter is outside the triangle, opposite the longest side for an acute triangle, the orthocenter is within the triangle. Along with the use of trigonometric relationships, the altitudes of a triangle can be used to determine many characteristics of triangles. Each of the altitudes of a triangle forms a right triangle, and the altitudes of a triangle all intersect at a point referred to as the orthocenter. The base of a triangle is determined relative to a vertex of the triangle the base is the side of the triangle opposite the chosen vertex.
Since all triangles have 3 vertices, every triangle has 3 altitudes, as shown in the figure below: Easy examples are Thales, Pythagoras, but also more advanced theorems like. An altitude of the isosceles triangle is shown in the figure below: GeoGebra's built-in theorem prover is already capable of proving geometrical statements in elementary planar geometry. In other words, an altitude in a triangle is defined as the perpendicular distance from a base of a triangle to the vertex opposite the base. In a triangle however, the altitude must pass through one of its vertices, and the line segment connecting the vertex and the base must be perpendicular to the base. In other geometric figures, such as those shown above (except for the cone), the altitude can be formed at multiple points in the figure.
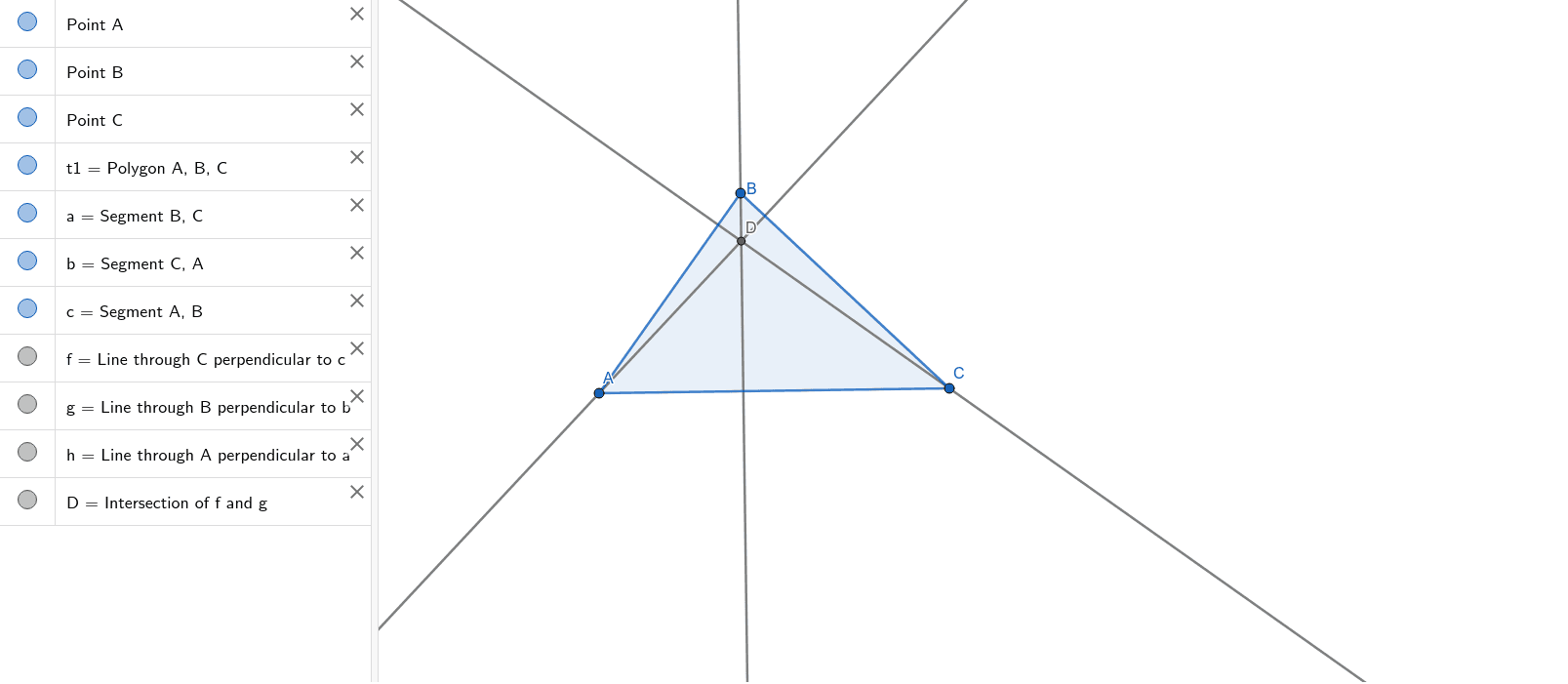
Altitude in trianglesĪltitude in triangles is defined slightly differently than altitude in other geometric figures. Note that the altitude can be depicted at multiple points within the figures, not just the ones specifically shown. By drawing an altitude from the right angle vertex to the hypotenuse of a. In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex). Similarly draw one more median to get the location of the centroid.The dotted red lines in the figures above represent their altitudes. You will use the GeoGebra geometry tool to explore how a line parallel to one. We just have to unhide the midpoints(if you had kept them hidden).Īfter they are visible again, use the Segment tool to connect a vertex with the midpoint on the opposite side. But we have already done that in the second step, we used the midpoints to draw the nine-point circle. So first we can use the Midpoint or Center tool to find/mark the midpoints on the sides. But we can use the Segment tool to draw a median.Ī median is a line segment joining a vertex to the midpoint on the opposite side. The perpendicular bisector of a triangle is formed by constructing perpendicular bisectors of each side of the triangle. I did not find a tool that will help us directly draw a median like the Perpendicular Line tool for an altitude. Geogebra Demonstration of Perpendicular BisectorsVocabular圜ircumcenter of the triangle the point of concurrency of the perpendicular bisectors.CircumcenterThe. Concurrence of the Altitudes As Seen from 3D Java, GeoGebra 3D Quadrilateral - a Coffin Problem. Centroid is the point where the three medians of a triangle intersect. 3 Roads, 3 Travelers Java 3 Utilities Puzzle. You can hide the altitudes after you have marked the orthocenter. Mark this point using the Intersect tool in the basic tools section and clicking on the two altitudes. The third altitude will also pass through the same point but we don’t need to draw it as we already have found out where they are intersecting. To find the midpoint of any side, say AB, just click on the vertices A and B in any order. Select the triangle tool and create an acute, scalene triangle. Once this tool is selected, find the midpoints of the three sides of your triangle. You will be constructing 3 altitudes in one triangle. Select the tool Midpoint or Center under the Construct section. Since midpoints are the easiest to find we will use them to draw this circle. Any three of them will do because only three points(non-collinear) are needed to construct a circle.
Midpoints of line segments from the vertices to the orthocenter of the triangle.īut to draw the nine-point circle, we don’t require all of the nine points. The nine-point circle of a triangle is a circle passing through the following nine points : But first we are going to need the nine-point circle whose center is the nine-point center. Step 2 : Constructing the nine-point center. (I have kept the axes and the grid hidden in the graph for the clarity of picture) Click again on the first point you made to finish forming the triangle. This is probably the easiest way to draw any casual triangle. To draw a triangle, click on any three different spots in the graphing panel to the right to mark the locations of the three vertices of the triangle.


 0 kommentar(er)
0 kommentar(er)
